AC Generators
AC generators are opposite from motors, because they convert mechanical energy into that of electrical. Mechanical energy is used to rotate the loops in the magnetic field, and the generated emf is a sine wave that varies in time. Steam made from burning fossil fuels such as coal, oil and natural gas is a common source in countries like the United States. In Europe, nuclear fission is used to create steam. In some hydroelectric plants, such as those found at Niagara Falls, water pressure is used to rotate the turbines. Turbines are rotors with vanes or blades. Wind and water are not commonly used as fossil fuels for mechanical energy sources because they are not as efficient and are more costly.
AC Motors
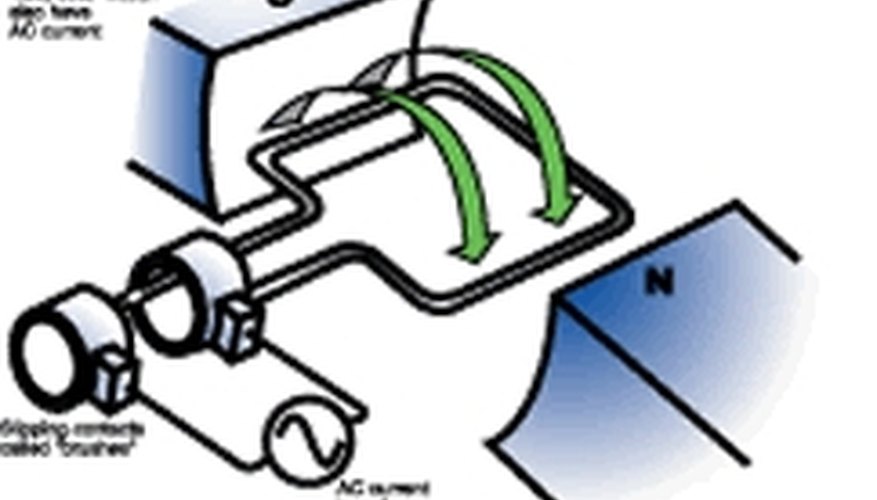
AC motors convert electrical energy into that of mechanical. An alternating current is used to rotate the loops in the magnetic field. Most AC motors produce the current by using induction. An electromagnet causes the magnetic field and uses the same voltage as the coils do.
DC Motors and Generators
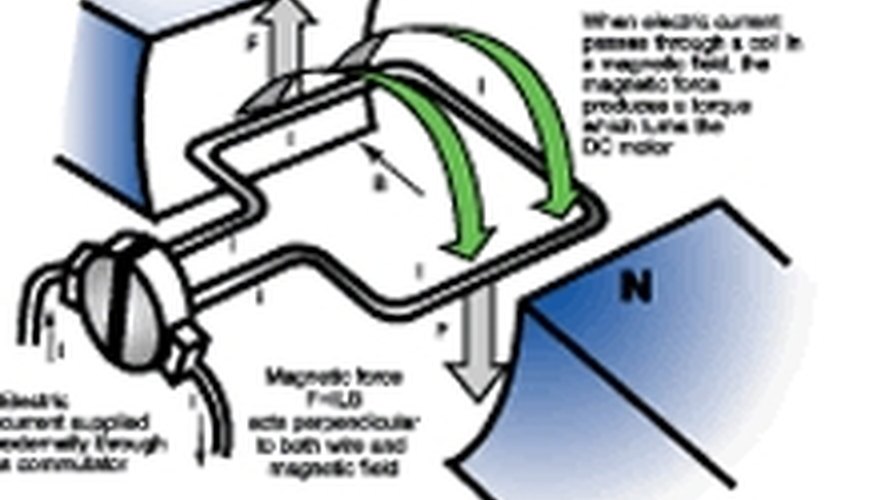
DC motors and generators are similar to their AC counterparts, except that they have a split ring called a commutator. The commutator is attached to electrical contacts called brushes. The changing direction of the current through the commutator causes the armature and thus the loops to rotate. The magnetic field the armature turns in may be a permanent magnet or electromagnet. DC generators have a generated emf is direct current.
Motors Compared to Generators
All motors are generators. The emf in a generator increases its efficiency, but an emf in a motor contributes to energy waste and inefficiency in its performance. A back emf is a resistance to change in a magnetic field. A back emf appears in a motor after it has been turned on, though not immediately. It reduces the current in the loop, and gets larger as the speed of the motor increases.This causes the power requirements of the motor to also increase, especially under loads that are very large.








